Assignment 2
- Name: Aadam
- Class: INFO-B 518
- Assignment: 2
a. What is the chance of getting 1 when rolling a die? (0.5 pts)
The chance of rolling a \(1\) on a fair six-sided die is \(1/6\).
b. Consider rolling two fair dice. What is the chance of getting two 1s? (0.5 pts)
The chance of getting two \(1\)s on two fair die is \((1/6) * (1/6) = 1/36 = 2.78\%\).
Determine if the statements below are true or false, and explain your reasoning.
(a) Assume that a couple has an equal chance of having a boy or a girl. If a couple’s previous three children have all been boys, then the chance that their next child is a boy is somewhat less than 50%. (1 pt)
False. The gender of each child is independent of the gender of the previous children. Therefore, the chance of having a boy or a girl remains approximately \(50\%\) for each subsequent child.
(b) Drawing a face card (jack, queen, or king) and drawing a red card from a full deck of playing cards are mutually exclusive events. (0.5 pts)
False. As we know that there are face cards (jacks, queens, kings) that could also be red, so it is possible to draw a card that is both red and a face card. That’s why this is not a mutually exclusive event.
(c) Drawing a face card and drawing an ace from a full deck of playing cards are mutually exclusive events. (1 pt)
True. There are no face cards that are also aces in a standard deck. So, it is not possible to draw a card that is both a face card as well as an ace card. That’s why this is a mutually exclusive event.
Red-green colorblindness is a common inherited form of colorblindness; the gene involved is transmitted on the X chromosome in a recessive manner. If a male inherits an affected X chromosome, he is necessarily colorblind (genotype XY). However, a female can only be colorblind if she inherits two defective copies (genotype XX-); heterozygous females are not colorblind. Suppose that a couple consists of a genotype XY male and a genotype X+ X-
(a) What is the probability of the couple producing a colorblind male? (1 pt)
The probability of the couple producing a colorblind male is \(50\%\) in this scenario. This is because the male in the couple would always contribute Y chromosome to the offspring, while the female could give either X+ or X-, which would result in the following combinations: (X+ Y) or (XY). So there’s a \(50\%\) chance that the male offspring would be colorblind.
(b) True or false: Among the couple’s offspring, colorblindness and female sex are mutually exclusive events (1 pt)
True. As we know that females could only be colorblind if she inherits two defective copies, but in this scenario, the male parent doesn’t have a defective copy, so there’s no chance that the female offspring would be colorblind. Only the male offsprings have a chance of being colorblind in this case.
In parts (a) and (b), identify whether the events are disjoint, independent, or neither (events cannot be both disjoint and independent).
(a) You and a randomly selected student from your class both earn A’s in this course. (1 pt)
If the instructor is using relative grading, then it’s neither independent nor disjoint, otherwise, it’s independent.
(b) You and your class study partner both earn A’s in this course. (0.5 pts)
Neither independent nor disjoint, because if you’re studying together, then some of the variables between you two would be correlated, such as study habits, which would suggest your course performance would also be related.
(c) If two events can occur at the same time, must they be dependent? (0.5 pts)
No. If two things are unrelated (independent), then one occurring does not have any effect on the other’s chance of occurring.
Data collected at elementary schools in DeKalb County, GA suggest that each year roughly 25% of students miss exactly one day of school, 15% miss 2 days, and 28% miss 3 or more days due to sickness.
a. What is the probability that a student chosen at random doesn’t miss any days of school due to sickness this year? (0.5 pts)
\[ P(\text{no misses}) = 1 - (0.25 + 0.15 + 0.28) = 0.32 \]
b. What is the probability that a student chosen at random misses no more than one day? (0.5 pts)
\[ P(\text{at most 1 miss}) = P(\text{no misses}) + P(\text{1 miss}) = 0.32 + 0.25 = 0.57 \]
c. What is the probability that a student chosen at random misses at least one day? (0.5 pts)
\[ P(\text{at least 1 miss}) = 1 - P(\text{no misses}) = 1 - 0.32 = 0.68 \]
d. If a parent has two kids at a DeKalb County elementary school, what is the probability that neither kid will miss any school? Note any assumptions made and evaluate how reasonable they are. (0.5 pts)
Assuming that both events are independent:
\[ P(\text{neither miss any}) = P(\text{no miss}) * P(\text{no miss}) = 0.32 * 0.32 = 0.1024 \]
Seat belt use is the most effective way to save lives and reduce injuries in motor vehicle crashes. In a 2014 survey, respondents were asked, “How often do you use seat belts when you drive or ride in a car?”. The following table shows the distribution of seat belt usage by sex.

(a) Calculate the marginal probability that a randomly chosen individual always wears seatbelts. (0.5 pts)
\[ 375264/436968 = 0.859 \]
(b) What is the probability that a randomly chosen female always wears seatbelts? (0.5 pts)
\[ 229246/436968 = 0.525 \]
(c) What is the conditional probability of a randomly chosen individual always wearing seatbelts, given that they are female? (0.5 pts)
\[ 229246/255980 = 0.896 \]
(d) What is the conditional probability of a randomly chosen individual always wearing seatbelts, given that they are male? (0.5 pts)
\[ 146018/180988 = 0.807 \]
(e) Calculate the probability that an individual who never wears seatbelts is male. (0.5 pts)
\[ 4719/7394 = 0.638 \]
(f) Does gender seem independent of seat belt usage? (0.5 pts)
No, there are certain trends that can be seen from the data based on gender. Even though the sample size of males is smaller than the females, we can see some interesting distributions, especially in the
Sometimes, Seldom, and Nevercategories.
Lupus is a medical phenomenon where antibodies that are supposed to attack foreign cells to prevent infections instead see plasma proteins as foreign bodies, leading to a high risk of blood clotting. It is believed that 2% of the population suffers from this disease. The test is 98% accurate if a person actually has the disease. The test is 74% accurate if a person does not have the disease. There is a line from the Fox television show House that is often used after a patient tests positive for lupus: “It’s never lupus.” Do you think there is truth to this statement? Use appropriate probabilities to support your answer.
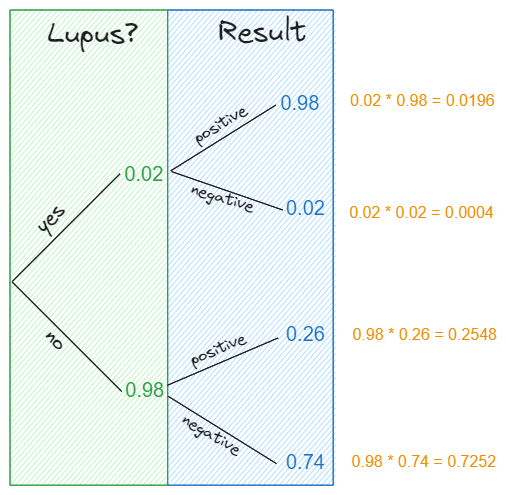
Let’s start by creating a tree diagram to better understand the probabilities:
Now let’s see the probability of a person getting a positive result given that he has a lupus:
\[P(\text{lupus} | \text{positive}) = \frac{P(\text{lupus} \land \text{positive})}{P(\text{positive})} = \frac{0.0196}{0.0196 + 0.2548} = 0.0714.\]
This means that even in the case where a patient tests positive for lupus, there is only a \(7.14\%\) chance that he actually has got the lupus. So even though House is not exactly right with the above statement, it still has some truth to it (skeptically).
Prostate-specific antigen (PSA) is a protein produced by the cells of the prostate gland. Blood PSA level is often elevated in men with prostate cancer, but a number of benign (not cancerous) conditions can also cause a man’s PSA level to rise. The PSA test for prostate cancer is a laboratory test that measures PSA levels from a blood sample. The test measures the amount of PSA in ng/ml (nanograms per milliliter of blood). The sensitivity and specificity of the PSA test depend on the cutoff value used to label a PSA level as abnormally high. In the last decade, 4.0 ng/ml has been considered the upper limit of normal, and values 4.1 and higher were used to classify a PSA test as positive. Using this value, the sensitivity of the PSA test is 20% and the specificity is 94%. The likelihood that a man has undetected prostate cancer depends on his age. This likelihood is also called the prevalence of undetected cancer in the male population. The following table shows the prevalence of undetected prostate cancer by age group.
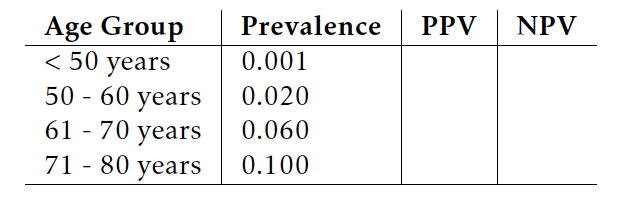
(a) Calculate the missing PPV and NPV values. (0.5 pts)
Age Group Prevalence PPV (%) NPV (%) < 50 years 0.001 0.33 99.91 50 - 60 years 0.020 6.37 98.29 61 - 70 years 0.060 17.54 94.85 71 - 80 years 0.100 27.03 91.36
(b) Describe any trends you see in the PPV and NPV values. (0.5 pts)
We can see that as the prevalence of the event increases, the PPV increases along with it, while the NPV starts decreasing.
(c) Explain the reason for the trends in part b), in language that someone who has not taken a statistics course would understand. (0.5 pts)
As men age, the chance of having prostate cancer increases (higher prevalence), so if a test says that you have cancer, the chance of it actually being true also increases (PPV increases). At the same time, if a test says that you don’t have cancer, the chance of if actually being wrong also increases (NPV decreases).
(d) The cutoff for a positive test is somewhat controversial. Explain, in your own words, how lowering the cutoff for a positive test from 4.1 ng/ml to 2.5 ng/ml would affect sensitivity and specificity. (0.5 pts)
Reducing the threshold for a positive PSA test result from 4.1 ng/ml to 2.5 ng/ml would make the test more sensitive in detecting prostate cancer but less specific in accurately identifying those without the disease. This adjustment could result in more men being recommended for additional tests, potentially including those who do not have prostate cancer (raising the number of false positives) while also identifying more instances of genuine prostate cancer cases (lowering the number of false negatives).
One of the earliest models for the genetics of eye color was developed in 1907, and proposed a single-gene inheritance model, for which brown eye color is always dominant over blue eye color. Suppose that in the population, 25% of individuals are homozygous dominant (BB), 50% are heterozygous (Bb), and 25% are homozygous recessive (bb).
(a) Suppose that two parents have brown eyes. What is the probability that their first child has blue eyes? (0.5 pts)
If both parents are homozygous dominant (BB) then the probability for the offspring to have blue eyes (b) is \(0\%\).
If one of the parents is heterozygous (Bb), then the probability would still be \(0\%\) because brown eye color (B) is always dominant.
If both parents are heterozygous (Bb), then the probability of the offspring to have blue eyes (bb) would be \(25\%\).
(b) Does the probability change if it is now known that the paternal grandfather had blue eyes? Justify your answer. (0.5 pts)
Yes, it does. It tells us that the father carries a recessive blue eye gene (b), so instead of assuming him homozygous dominant (BB), we can consider him a heterozygous (Bb), which increases the probability of having the first child with blue eyes.
(c) Given that their first child has brown eyes, what is the probability that their second child has blue eyes? Ignore the condition given in part (b). (0.5 pts)
I believe that the probabilities would remain the same as in
(a), because it doesn’t really tell us much about the parents. They could still be both (BB), one of them (Bb), or both (Bb). So, the probabilities would remain the same.
The Behavioral Risk Factor Surveillance System (BRFSS) is an annual telephone survey designed to identify risk factors in the adult population and report emerging health trends. The following table displays the distribution of the health status of respondents to this survey (excellent, very good, good, fair, poor) conditional on whether or not they have health insurance.

(a) Are being in excellent health and having health coverage mutually exclusive? (0.5 pts)
No. There are \(20.99\%\) population that has both excellent health and health insurance. So these two variables aren’t mutually exclusive.
(b) What is the probability that a randomly chosen individual has excellent health? (0.5 pts)
\(0.2329\)
(c) What is the probability that a randomly chosen individual has excellent health given that he has health coverage? (0.5 pts)
\[\frac{0.2099}{0.8738} = 0.2402\]
(d) What is the probability that a randomly chosen individual has excellent health given that he doesn’t have health coverage? (0.5 pts) > \[\frac{0.0230}{0.1262} = 0.1822\]
(e) Do having excellent health and having health coverage appear to be independent? (0.5 pts) > If we look at the probabilities from (c) & (d) answers, we see that although the values are different, but not by a very big margin. They are close enough to one another. Based on that, these two variables appear to be independent.